1-1-1 離散数学

離散数学とは，コンピューターで数値を扱うための数学です。コンピュータ内部では0 と1の2 つの数値しか使えないので，データを表現するのに，様々な工夫が必要になります。

基数

基数とは，ある集合の要素の個数を表す自然数です。例えば，人間は一般的には，

{0，1，2，3，4，5，6，7，8，9}

の10 種類の数字を使って数値を表現する，10 進数を使います。コンピュータでは，電気のONとOFFを組み合わせて，

{0，1}

の2 種類で数値を表現する，2 進数が使われます。

コンピュータで数値を計算するためには，10 進数から2 進数にする必要があります。このように，基数を変える演算を基数変換といいます。

2 進数から10 進数への基数変換

2 進数から10 進数への基数変換は，各位の値に2 の何乗かをかけて全部足すことで求められます。

例えば，2 進数の10111(2) を10 進数に基数変換するには，次のように計算します。

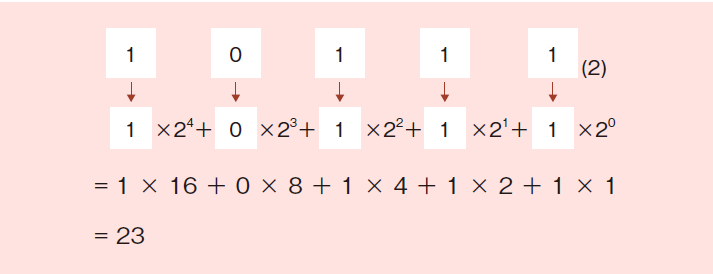
計算結果の23が，10進数に変換した値となります。

10進数から2進数への基数変換

10進数から2進数への基数変換は，10進数の数を順に2で割っ
ていき，余りを下から順に並べることで求められます。
例えば，10進数の23を2進数に基数変換するには，次のよう
に計算します。

商が0になるまで続けた後，余りを下から並べた，10111(2)が，
2進数に変換した値となります。

小数の場合

小数の場合にも，基数変換を行うことができます。

2 進数から10 進数に変換する場合には，小数点第1位は2-1，小数点第2 位は2-2というかたちになるので，整数の場合と同様に計算できます。

例えば，2 進数の10.11(2)を10進数に基数変換するには，次のように計算します。

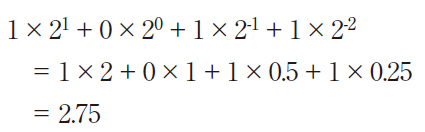
10 進数から2進数へ計算するときには，2で割るのではなく，2を掛けていき，整数部分を上から順に並べることで求められます。
例えば，10進数の0.75を2進数に基数変換するには，次のように計算します。

小数部分が0になるまで続けた後，整数部分を上から並べた，0.11(2)が，2進数に変換した値となります。
n進数・16進数
基数は，2や10 以外の，任意の自然数が使用できます。基数がnの数を，n進数と表します。n進数として，2進数や10進数以外で最もよく使われるのが，
{0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F}
の16種類の数字を使った16進数です。16=24で，2進数の4桁が
16進数の1桁に対応するので，2進数との基数変換が簡単にでき
るからです。
0 ～ 16までの，2進数，10進数，16進数の対応をまとめると，次のようになります（2進数は，最低4桁で，0を埋めています）。

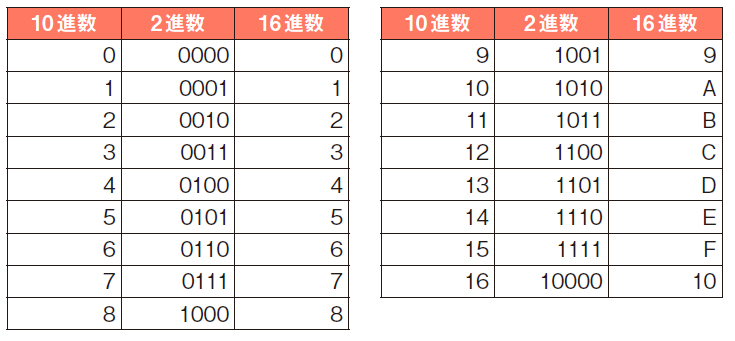
数値の表現

コンピュータの中では，データはすべて0と1で表現します。
負の数や小数をコンピュータ内で表現するには，工夫が必要で
す。

負の数の表現

コンピュータの中では，負の数を表現するときに，補数を利用します。補数とは，ある自然数に対して，足すと1桁増える最も小さな数です。
例えば，4ビットの2 進数である 0110(2)の補数を考えます。2進数4桁の 0110(2)の補数は，足すと10000(2)になる2進数なので，次の式で計算できます。

2進数の補数は，次のような2 段階の計算で求めることもできます。
①各桁の0と1を反転する

②①の値に1を足す

補数を使った減算

補数を使って計算することで，コンピュータの内部では減算もすべて加算で行うことができます。減算用の回路を用意する必要がなくなり，演算回路が簡単になるというメリットがあります。
例えば，補数を使って4ビットの2進数 0110(2)−0011(2)の計算を行う場合を考えます。まず，0011(2)の補数を求めると，次のようになります。

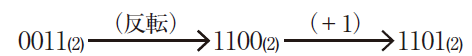
求めた補数を足して，桁上がりを無視すると，減算と同じ結果となります。

小数の表現

コンピュータで小数を表現するためには，次のような方法があります。
●固定小数点数
小数点の位置を固定して，桁数を指定して表現する方法です。
●浮動小数点数
小数点の位置を固定せず，指数部と仮数部に分けて表現する方法です。
●BCD（Binary Coded Decimal：2進化10進）
10進数の1桁ごとに，2進数に変換して表現する方法です。
現在のコンピュータで最もよく使われているのが，浮動小数点数です。浮動小数点数では，次のようなかたちで，小数部分を含む実数を表します。

[符号部][指数部]×[仮数部]

10進数での浮動小数点の表し方は，符号は＋か−，指数は10の何乗というかたち，仮数は最上位の桁が1桁になるように調整した小数です。例えば，0.75 と−37.5 を，10進数で浮動小数点にすると，次のようになります。

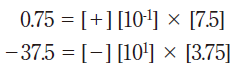
2進数での浮動小数点の表し方は，基本的には10 進数と同じです。コンピュータで取り扱うためには，すべて0と1で表現する必要があるので，次のような工夫を行います。

実際に使われている浮動小数点には，符号部1ビット，指数部8ビット，仮数部23ビットの合計32ビットで表現する単精度浮動小数点数や，符号部1ビット，指数部11ビット，仮数部52ビットの合計64ビットで表現する倍精度浮動小数点数などがあります。
単精度浮動小数点数での，数値の表現形式は，次のようにな
ります。

指数部には，実際の指数に127を加えた値を2進数で設定しま
す。
例えば，0.625を単精度浮動小数点数で表現する場合を考えてみます。まず，0.625を2進数に直すと，次のようになります。

0.101(2)は，2進数の浮動小数点では，次のように表されます。

符号部は，正なので0となります。指数部は，−1なので，127を加えて2進数にすると，次のようになります。

仮数部は，最上位の1 は省略し，小数部分の01 を使用します。残りの桁は0 を設定すると，23 ビットで1000000000000000000000となります。
これらの値を順番に並べると，次のようになります。

算術演算と精度

コンピュータの内部では，算術演算は，すべて0と1のビットを使って実行します。加算は高速で行えますが，減算，乗算，除算は遅くなるので工夫が必要です。
減算は2の補数を使って加算に直す方法が使われます。乗算，除算では，シフト演算を組み合わせることで，高速な演算を実現できます。

シフト演算

シフト演算とは，ある2進数のすべてのビットを特定のビット数だけ右や左にずらすことです。
例えば，0000001(2)という2進数があるとき，左に2ビットだけシフトすると，0000100(2)となります。
1ビット左シフトするごとに数が2倍になり，1ビット右シフトするごとに数が1/2になります。2ビット左シフトした場合は，2×2=4倍になります。ずらして格納できなくなったビットは無視されます。

シフト演算の方法には，論理シフトと算術シフトの2種類があ
ります。

●論理シフト
論理シフトは，ずらして空いた部分に，0を補充するシフトです。右シフトでも左シフトでも，空いた部分に0を設定します。

例えば，1000001(2)を1ビット論理右シフトすると0100000(2)，1ビット論理左シフトすると，0000010(2)となります。
●算術シフト
算術シフトは，右シフトを行うときに，空いた部分に一番左の値と同じものを設定するシフトです。これは，2の補数などで負の数を表現する場合に対応したものです。負の数の場合，左端のビットが1になっているので，1を補充することで，マイナスのまま値をシフトできます。左シフトは0を補充するので論理シフトと同じ値になります。
例えば，1000001(2)を1ビット算術右シフトすると1100000(2)となります。

表現可能な数値の範囲

コンピュータで数値を表現する場合，1つの数値に確保されたビット数はデータ型によって決まっており，限りがあります。また，負の数を表す（符号付き）か，0以上の数に限る（符号なし）かで表現できる数も変わってきます。
例えば，8ビットで負の数も含めた整数を表す8ビット整数型の場合は，最大値は01111111(2)で10 進数の127になります。最小値は負の数の2の補数表現で10000000(2)となり，10 進数に直すと−128です。
●オーバーフロー
最大値01111111(2)で，より大きい値を表そうと，127に＋1をすると10000000(2)となってしまいます。これは，2の補数表現で−128を表すこととなり，計算がおかしくなります。この現象をオーバーフロー（あふれ）といいます。

●アンダーフロー
浮動小数点では，指数部と仮数部を使って小数を表現します。実は，浮動小数点では，完全な0は表現できません。単精度浮動小数点数では，指数部を0にしても，2-127までしか小さくなりません。これより小さく，0に近い値は単精度浮動小数点数として表現することができません。この現象をアンダーフローといいます。

演算精度

データをコンピュータ内部で格納するときには，ビットの数が限られており，有効数字が決まっています。有効な桁数を超えた数値を格納できず，実際のデータとの誤差が生じることを，丸め誤差といいます。丸め誤差は，有効桁数が多いほうが少なくなります。例えば，浮動小数点のデータの場合，32ビットの単精度浮動小数点よりは，64ビットの倍精度浮動小数点のほうが精度が高く，丸め誤差も小さくなります。
また，単純な数値の誤差だけではなく，演算によって情報が欠落することがあります。情報の欠落の代表的なものに，桁落ちと情報落ちがあります。

●桁落ち
値がほぼ等しい2つの数値の差を求めたとき，有効数字の桁数である有効桁数が減ることによって発生する誤差です。

●情報落ち
絶対値が非常に大きな数値と小さな数値の足し算や引き算
を行ったとき，小さい数値が計算結果に反映されないことに
よって発生する誤差です。

演算の精度を上げるためには，桁落ちや情報落ちの発生を防ぐように，計算順序などを工夫することが大切です。

集合と命題

集合と命題は，コンピュータで論理を表すときの基本となる考え方です。プログラミングでは，集合を考え，命題を条件で判定するので，集合を正確に理解することが重要になります。

集合

範囲がはっきりしているものの集まりを，集合といいます。集合を構成している1つひとつのものを，その集合の要素または元といいます。
集合を表すには，次の2つの方法があります。
①要素を1つひとつ書き並べる
要素の内容を1つひとつ並べるやり方です。例えば，10 進数で使える数字を表すとき，{0，1，2，3，4，5，6，7，8，9}と並べて表現します。
②要素の満たす条件を示す
要素を満たす条件を示すやり方です。例えば，10進数で使える数字を，「0から9までの整数」と，条件を記述することで表現します。

命題

正しいか正しくないかが明確に決まる式や文章を，命題といいます。命題が正しいことを，真であるといい，正しくないことを，偽であるといいます。

集合の表し方

集合を視覚的にわかりやすく表すために，ベン図という図が用いられます。
例えば，2つの集合A，B で，Aのどの要素もB であるとき，AはBの部分集合であるといいます。部分集合は，ベン図で次のように表されます。

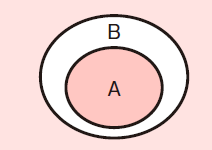
また，集合を考えるときの対象の範囲全体の集合を，全体集合といいます。
集合を組み合わせたときの代表的なものに，次の5つがあります。ベン図だけでなく，AND（・，∩，∧）やOR（＋，∪，∨）などの記号を用いて表すこともあります。
ここでは，例として，集合A「コーヒーが好きな人」，集合B「紅茶が好きな人」とします。
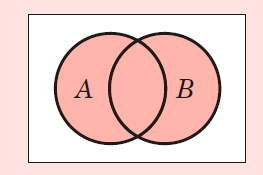
①和集合
2つの集合を足したものです。例では，「コーヒーか紅茶が好きな人」になります。

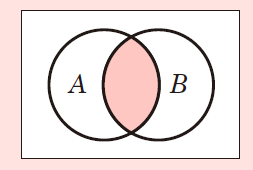
②積集合
2つの集合の両方に当てはまるものです。例では，「コーヒーも紅茶も好きな人」になります。

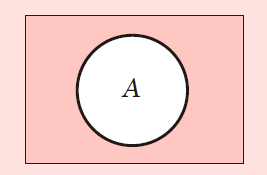
③補集合
全体集合の否定です。例では，「コーヒーが好きではない人」になります。

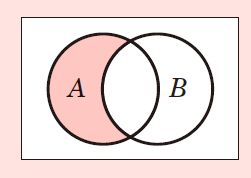
④差集合（A－B）
ある集合から，別の集合の条件にあてはまるものを引いたものです。例では，「コーヒーは好きだけれど紅茶は好きではない人」になります。

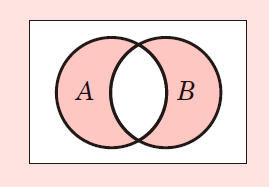
⑤対称差集合
2つの集合のうち，どちらかの条件にあてはまるものから，両方の条件にあてはまるものを引いたものです。前記の例では，「コーヒーか紅茶が好き，しかし両方は好きではない人」になります。

論理演算

コンピュータの表現では，数値のほかに論理（真か偽か）も表現できます。論理演算とは，命題を論理で表現し，その組み合わせを演算することです。

論理演算の基本

基本的な論理演算には，次の3つがあります。
●論理和（A or B，A＋B， A∪B，A∨B）
2つの命題A,Bがあるとき，A「または」B，またはその両方，という言葉で表される複合命題を，論理和といいます。プログラムでは，or（または OR）で表現されることが多いです。
●論理積（A and B，A・B，A∩B，A∧B）
2つの命題A,Bがあるとき，A「かつ」Bという言葉で表される複合命題を，論理積といいます。プログラムでは，and（または AND）で表現されることが多いです。

_
●否定（not A，A）
命題Aがあるとき，A「ではない」という言葉で表される命題を，否定といいます。プログラムでは，not（または NOT）で表現されることが多いです。

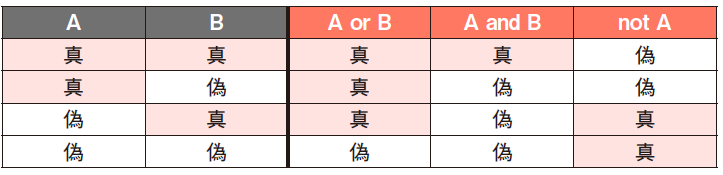
真理値表

論理演算の値の組合せを表現する方法に，真理値表があります。論理和，論理積，否定の真理値表は，次のように表現されます。

その他の論理演算

論理演算には，論理和，論理積，否定以外にも，次のようなものがあります。

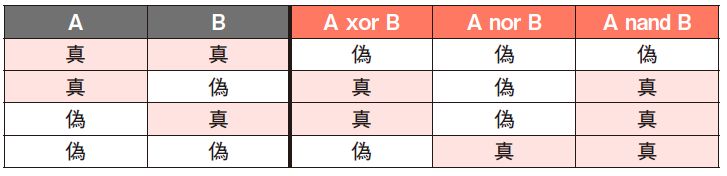
●排他的論理和（A xor B，A⊕B，A△B）
2つの命題A,Bがあるとき，A「または」B，という言葉で表され，「AとBの両方」を含まない複合命題を，排他的論理和といいます。

____
●否定論理和（A nor B，A∪B）
論理和の否定です。AまたはB「ではない」，つまり，AでもBでもない場合にあてはまります。

_____
●否定論理積（A nand B，A∩B）
論理積の否定です。AかつB「ではない」，つまり，AとBの両方ではない場合にあてはまります。

論理演算の法則

論理演算が従う法則には，様々なものがあります。知っておくと便利な法則には，次のようなものがあります。